Java中的图表
1.概述
在本教程中,我们将了解一下图作为数据结构的基本概念。
我们还将探讨它在Java中的实现,以及在图上可能的各种操作。我们还将讨论提供图形实现的Java库。
2.图形数据结构
图是一种数据结构,用于存储连接的数据,如社交媒体平台上的人际关系网。
一个图由顶点和边组成。一个顶点代表实体(如人),一条边代表实体之间的关系(如一个人的朋友关系)。
让我们定义一个简单的图表,以更好地理解这一点:
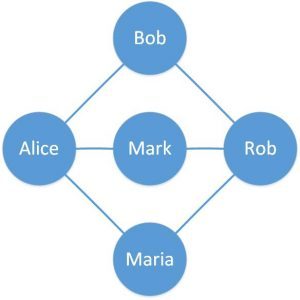
这里我们定义了一个有五个顶点和六条边的简单图形。圆圈是代表人的顶点,连接两个顶点的线是代表在线门户的朋友的边。
根据边的属性,这个简单的图有一些变化。让我们在接下来的章节中简单介绍一下。
然而,在本教程的Java例子中,我们将只关注这里所介绍的简单图形。
2.1.有向图
到目前为止,我们所定义的图是没有任何方向的边。如果这些边有一个方向,产生的图就被称为有向图。
一个例子可以表示谁在在线门户上的友谊中发送了好友请求:
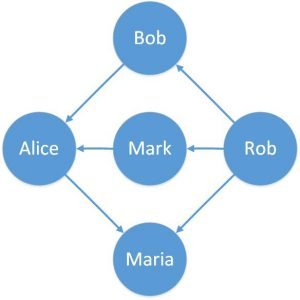
在这里我们可以看到,边缘有一个固定的方向。边缘也可以是双向的。
2.2.加权图
同样,我们的简单图的边是无偏差的或无权重的。
如果这些边带着相对的权重,这个图就被称为加权图。
实际应用的一个例子可以表示在线门户上的友谊的相对年龄:
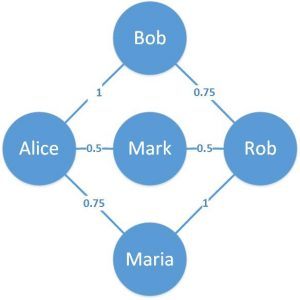
在这里我们可以看到边缘具有与其相关的权重。这为这些边缘提供了相对含义。
3.图形表示法
图可以用不同的形式表示,如邻接矩阵和邻接列表。在不同的设置中,每一种都有其优点和缺点。
我们将在本节中介绍这些图形表示。
3.1.邻接矩阵
邻接矩阵是尺寸等于图中顶点数量的方阵。
矩阵的元素通常具有值 0 或 1。值 1 表示行和列中的顶点之间相邻,否则值为 0。
让我们看看上一节中简单图的邻接矩阵是什么样的:
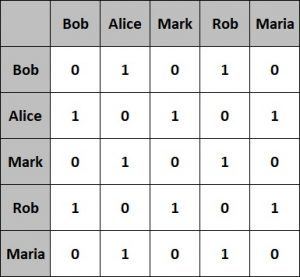
这种表示方式更容易实现并且查询效率更高。但是,在占用空间方面效率较低。
3.2.邻接列表
一个邻接列表只不过是一个列表的数组。数组的大小相当于图中顶点的数量。
数组中某一特定索引处的列表代表该数组索引所代表的顶点的相邻顶点。
让我们看看上一节中我们的简单图的邻接列表是什么样子的:
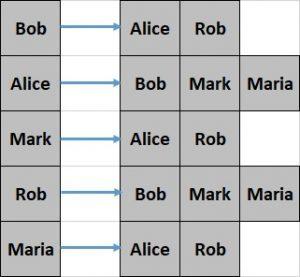
这种表示方式创建起来相对困难,而且查询效率较低。但是,它提供了更好的空间效率。
在本教程中,我们将使用邻接列表来表示图。
4.Java中的图表
Java没有一个默认的图数据结构的实现。
然而,我们可以用Java集合来实现图。
让我们从定义一个顶点开始:
class Vertex {
String label;
Vertex(String label) {
this.label = label;
}
// equals and hashCode
}上述顶点的定义只是以一个标签为特征,但这可以代表任何可能的实体,如Person或City。
此外,请注意我们必须覆盖equals()和hashCode()方法,因为这些方法是与Java集合一起工作所必需的。
正如我们前面所讨论的,图只不过是一个顶点和边的集合,可以用邻接矩阵或邻接列表来表示。
让我们看看我们如何在这里用邻接列表来定义这个问题:
class Graph {
private Map<Vertex, List<Vertex>> adjVertices;
// standard constructor, getters, setters
}正如我们所看到的,Graph类使用了Java集合中的Map来定义邻接列表。
在图数据结构上有几种可能的操作,例如创建、更新或搜索图。
我们将介绍一些更常见的操作,并了解如何在 Java 中实现它们。
5.图的改变操作
首先,我们将定义一些方法来改变图数据结构。
让我们来定义添加和删除顶点的方法:
void addVertex(String label) {
adjVertices.putIfAbsent(new Vertex(label), new ArrayList<>());
}
void removeVertex(String label) {
Vertex v = new Vertex(label);
adjVertices.values().stream().forEach(e -> e.remove(v));
adjVertices.remove(new Vertex(label));
}这些方法只是简单地从顶点集中添加和删除元素。
现在,让我们也定义一个方法来添加一个边缘:
void addEdge(String label1, String label2) {
Vertex v1 = new Vertex(label1);
Vertex v2 = new Vertex(label2);
adjVertices.get(v1).add(v2);
adjVertices.get(v2).add(v1);
}这个方法创建了一个新的Edge,并更新了相邻的顶点Map。
以类似的方式,我们将定义removeEdge()方法:
void removeEdge(String label1, String label2) {
Vertex v1 = new Vertex(label1);
Vertex v2 = new Vertex(label2);
List<Vertex> eV1 = adjVertices.get(v1);
List<Vertex> eV2 = adjVertices.get(v2);
if (eV1 != null)
eV1.remove(v2);
if (eV2 != null)
eV2.remove(v1);
}接下来,让我们看看如何使用我们到目前为止定义的方法来创建我们之前画的简单的图:
Graph createGraph() {
Graph graph = new Graph();
graph.addVertex("Bob");
graph.addVertex("Alice");
graph.addVertex("Mark");
graph.addVertex("Rob");
graph.addVertex("Maria");
graph.addEdge("Bob", "Alice");
graph.addEdge("Bob", "Rob");
graph.addEdge("Alice", "Mark");
graph.addEdge("Rob", "Mark");
graph.addEdge("Alice", "Maria");
graph.addEdge("Rob", "Maria");
return graph;
}最后,我们将定义一个方法来获取某个特定顶点的相邻顶点:
List<Vertex> getAdjVertices(String label) {
return adjVertices.get(new Vertex(label));
}6.遍历图形
现在我们已经定义了图的数据结构以及创建和更新它的函数,我们可以定义一些额外的函数来遍历图。
我们需要遍历一个图来执行任何有意义的操作,例如在图中进行搜索。
有两种可能的方式来遍历图:深度优先遍历和广度优先遍历。
6.1.深度优先遍历
一个深度优先的遍历从一个任意的根顶点开始,沿每个分支尽可能深入地探索顶点,然后再探索同一级别的顶点。
让我们定义一个方法来执行深度优先的遍历:
Set<String> depthFirstTraversal(Graph graph, String root) {
Set<String> visited = new LinkedHashSet<String>();
Stack<String> stack = new Stack<String>();
stack.push(root);
while (!stack.isEmpty()) {
String vertex = stack.pop();
if (!visited.contains(vertex)) {
visited.add(vertex);
for (Vertex v : graph.getAdjVertices(vertex)) {
stack.push(v.label);
}
}
}
return visited;
}在这里,我们使用一个栈来存储需要遍历的顶点。
让我们在上一小节中创建的图形上运行这个程序:
assertEquals("[Bob, Rob, Maria, Alice, Mark]", depthFirstTraversal(graph, "Bob").toString());请注意,我们在这里使用顶点“Bob”作为我们的遍历根,但这也可以是任何其他顶点。
6.2.广度优先遍历
相对而言,广度优先遍历从一个任意的根顶点开始,在深入到图中之前,先探索同一层次的所有相邻顶点。
现在我们定义一个方法来执行广度优先遍历:
Set<String> breadthFirstTraversal(Graph graph, String root) {
Set<String> visited = new LinkedHashSet<String>();
Queue<String> queue = new LinkedList<String>();
queue.add(root);
visited.add(root);
while (!queue.isEmpty()) {
String vertex = queue.poll();
for (Vertex v : graph.getAdjVertices(vertex)) {
if (!visited.contains(v.label)) {
visited.add(v.label);
queue.add(v.label);
}
}
}
return visited;
}请注意,广度优先遍历利用队列来存储需要遍历的顶点。
让我们在同一张图上再次运行此遍历:
assertEquals(
"[Bob, Alice, Rob, Mark, Maria]", breadthFirstTraversal(graph, "Bob").toString());同样,根顶点(此处为“Bob”)也可以是任何其他顶点。
7. 用于图形的 Java 库
没有必要总是在 Java 中从头开始实现图。有几个开源和成熟的库可以提供图形实现。
在接下来的几小节中,我们将介绍其中一些库。
7.1. JGraphT
JGraphT 是 Java 中最流行的图形数据结构库之一。它允许创建简单图、有向图和加权图等。
此外,它还提供了许多关于图数据结构的可能算法。我们之前的教程之一更详细地介绍了 JGraphT。
7.2. Google Guava
Google Guava 是一组 Java 库,提供一系列功能,包括图形数据结构及其算法。
它支持创建简单的Graph、ValueGraph和Network。它们可以定义为可变或不可变。
7.3. Apache Commons
Apache Commons 是一个提供可重用 Java 组件的 Apache 项目。这包括 Commons Graph,它提供了一个用于创建和管理图形数据结构的工具包。这也提供了对数据结构进行操作的通用图算法。
7.4. Sourceforge JUNG
Java Universal Network/Graph (JUNG)是一个Java框架,为任何可以表示为图的数据的建模、分析和可视化提供可扩展的语言。
JUNG支持许多算法,其中包括聚类、分解和优化等例程。
这些库提供了一些基于图数据结构的实现。还有更强大的基于图的框架,比如Apache Giraph,目前在Facebook用于分析其用户形成的图,以及Apache TinkerPop,常用于图数据库之上。
8.结语
在这篇文章中,我们讨论了作为数据结构的图及其表示方法。我们在Java中使用Java集合定义了一个非常简单的图,还为图定义了常见的遍历方法。
我们还简要地谈到了在Java平台之外的各种提供图实现的库。
像往常一样,这些例子的代码可以在GitHub上找到。